Привет, дорогие слушатели! Сегодня мы поговорим о двух важных типах распределений вероятностей для непрерывных случайных величин: равномерном и экспоненциальном. Эти распределения часто встречаются в различных областях науки и практики, таких как теория надежности, теория очередей, статистика, физика и другие. Мы рассмотрим их основные свойства, характеристики, примеры и приложения. 😊
Видео:Теория вероятностей #12: случайная величина, плотность и функция распределенияСкачать

🔹 Что такое непрерывная случайная величина? 🔹
Начнем с определения того, что такое непрерывная случайная величина. Это такая случайная величина, которая может принимать любые значения из некоторого интервала или множества интервалов на числовой прямой. Например, время жизни лампочки, длина стержня, скорость автомобиля, температура воздуха и т.д. 😎
Для непрерывной случайной величины X X не существует функции вероятности, то есть нельзя сказать, какова вероятность того, что X X равна какому-то конкретному числу. Ведь вероятность того, что X X попадет в любую точку на числовой прямой, равна нулю. Вместо этого, для непрерывной случайной величины X X определяют функцию распределения F ( x) F(x) и плотность распределения f ( x) f(x) . 😯
Функция распределения F ( x) F(x) показывает, какова вероятность того, что X X не превысит заданного значения x x , то есть F ( x) = P ( X ≤ x) F(x)=P(Xleqslant x) . Функция распределения F ( x) F(x) имеет следующие свойства:
- Она неубывающая, то есть если x 1 < x 2 x_1<x_2 ,="" то="" f="" (="" x="" 1)="" ≤="" 2)="" f(x_1)leqslant="" f(x_2)="" ;
- Она ограниченная, то есть 0 ≤ F ( x) ≤ 1 0leqslant F(x)leqslant 1 для любого x x ;
- Она непрерывная, то есть не имеет скачков;
- Она стремится к нулю при x → − ∞ xto -infty и к единице при x → + ∞ xto +infty .
Плотность распределения f ( x) f(x) определяется как производная функции распределения F ( x) F(x) по x x , то есть f ( x) = F ′ ( x) f(x)=F’(x) . Плотность распределения f ( x) f(x) имеет следующие свойства:
- Она неотрицательная, то есть f ( x) ≥ 0 f(x)geqslant 0 для любого x x ;
- Она нормированная, то есть её интеграл по всей числовой прямой равен единице, то есть ∫ − ∞ + ∞ f ( x) d x = 1 int_{-infty}^{+infty}f(x)dx=1 ;
- Она характеризует плотность вероятности в окрестности точки x x , то есть вероятность того, что X X попадет в некоторый малый интервал ( x , x + Δ x) (x,x+Delta x) , приблизительно равна f ( x) Δ x f(x)Delta x .
Зная плотность распределения f ( x) f(x) , можно найти функцию распределения F ( x) F(x) , интегрируя плотность от минус бесконечности до x x , то есть F ( x) = ∫ − ∞ x f ( t) d t F(x)=int_{-infty}^{x}f(t)dt . Обратно, зная функцию распределения F ( x) F(x) , можно найти плотность распределения f ( x) f(x) , дифференцируя функцию распределения по x x , то есть f ( x) = F ′ ( x) f(x)=F’(x) . 😁
Видео:Нормальное Распределение за 6 МинутСкачать

🔹 Что такое равномерное распределение? 🔹
Равномерное распределение — это такое распределение вероятностей для непрерывной случайной величины X X , при котором X X может принимать любые значения из некоторого интервала [ a , b] [a,b] с одинаковой вероятностью. То есть, вероятность того, что X X попадет в любой подынтервал [ a , b] [a,b] , пропорциональна длине этого подынтервала. 😮
Например, если X X — это длина стороны квадрата, то X X может быть любым числом от 0 0 до 10 10 сантиметров с одинаковой вероятностью. Если X X — это температура воды в бассейне, то X X может быть любым числом от 20 20 до 30 30 градусов Цельсия с одинаковой вероятностью. Если X X — это время прибытия автобуса на остановку, то X X может быть любым числом от 9:00 9:00 до 9:15 9:15 с одинаковой вероятностью. 😊
Равномерное распределение обозначается как U ( a , b) U(a,b) , где a a и b b — это границы интервала, на котором определена случайная величина X X . Плотность распределения равномерного распределения имеет вид:
Функция распределения равномерного распределения имеет вид:
F(x)={0,если xb.F(x)=begin{cases}
0, & text{если } xb.
end{cases}
F(x)=⎩⎨⎧0,b−ax−a,1,если xb.
Графики плотности и функции распределения равномерного распределения U ( 0 , 1) U(0,1) выглядят так:
🎬 Видео
Экспоненциальное (показательное) распределение непрерывной случайной величины.Скачать

Равномерное распределение случайной величиныСкачать

Функция распределения непрерывной случайной величины. Вероятность попадания в интервалСкачать

Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать

Равномерное распределениеСкачать

Теория вероятностей #18: системы двух случайных величин, двумерное распределениеСкачать

Законы распределения непрерывных случайных величинСкачать
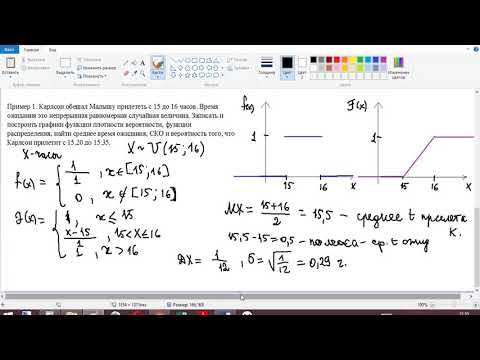
Равномерное распределение непрерывной случайной величины.Скачать

Показательное распределениеСкачать

Биноминальное распределениеСкачать

Функция распределения и плотность распределенияСкачать

Функция распределения дискретной случайной величиныСкачать

Непрерывное равномерное распределение плотности вероятностиСкачать

Равномерное и показательное распределениеСкачать
Нормальное распределениеСкачать

Теория вероятностей #19: ковариация, корреляция, зависимость двух случайных величинСкачать

14 Непрерывные случайные величины ЗадачиСкачать

ТВиМС. 7 Основные законы распределения случайных величинСкачать