Пусть имеется полная группа несовместных событий — гипотез $Н_1, Н_2,dots , Н_n$. Вероятности этих гипотез до опыта известны и равны соответственно: $Pleft(H_{1}
ight),Pleft(H_{2}
ight),…,Pleft(H_{n}
ight)$.
Произведен опыт, в результате которого событие А появилось. Какие вероятности получат гипотезы в связи с появлением события А. По-другому будем искать условные вероятности $Pleft({
aise0.7exhbox{$ H_{i} $} left/{vphantom{H_{i} A}}
ight.lower 0.7exhbox{$ A $}}
ight)$ для каждой гипотезы.
- Теорема Байеса
- Использование формулы Байеса при решении задач
- Реферат: Формула полной вероятности и формула Бейеса Байеса и их применение
- 1. Формула полной вероятности
- 2. Формула Байеса( Бейеса)
- 4. Основные сферы применения формулы Байеса(Бейеса)
- Формула полной вероятности. Формулы Бейеса. Примеры решения задач
- Примеры решения задач по теме «Формула полной вероятности. Формулы Бейеса»
- Другие статьи по данной теме:
- Как применять теорему Байеса для решения реальных задач
- Формула Байеса
- Пример
- Визуализация вероятности
- Что, если есть еще больше данных?
- Заключение
- Формула полной вероятности и формула Бейеса Байеса и их применение
- 1. Формулаполной вероятности
- 2. ФормулаБайеса( Бейеса)
- 4.Основные сферы применения формулыБайеса(Бейеса)
- 🔥 Видео
Теорема Байеса
Теорема
Вероятность гипотезы при условии, что событие А произошло, равна произведению вероятности этой гипотезы на соответствующую ей условную вероятность события А, которое произошло при испытании, деленному на полную вероятность события А.
Доказательство
Согласно теореме умножения для двух событий
$$P(AH_i)=P(A) cdot P (H_i/A)=P(H_i) cdot P(A/H_i)$$
Откуда
Выразив $Р(А)$ получим формулу:
которая носит название формулы Байеса. Теорема доказана.
Ничего непонятно?
Попробуй обратиться за помощью к преподавателям
Использование формулы Байеса при решении задач
Пример 1
Каждый из двух стрелков независимо друг от друга произвел выстрел по некоторому объекту. Вероятность попадания в цель первым стрелком равна 0,7; вторым — 0,6. Объект поражен одним попаданием. Определить вероятность того, что объект поражен первым стрелком.
Решение.
Обозначим событие А — поражение объекта одним попаданием. Для опыта виделим следующие гипотезы:
$Н_1$ — стрелки не попадают;
$Н_2$ — стрелки одновременно попадают;
$Н_3$ — первый стрелок попадет, второй — нет;
$Н_4$ — второй стрелок попадет, первый — нет.
Найдем вероятность этих гипотез:
$P(H_1)=0,3•0,4=0,12,$
$$P(H_2)=0,7•0,6=0,42,$$ $$P(H_3)=0,7•0,4=0,28,$$ $$P(H_4)=0,3•0,6=0,18.$$
Найдем условные вероятности события А при этих гипотезах:
$$P(A/H_1)=0$$$$P(A/H_2)=0$$$$P(A/H_3)=1$$$$P(A/H_4)=1$$
После опыта гипотезы $Н_1$ и $Н_2$ становятся невозможными, а вероятности гипотез $Н_3$ и $Н_4$ будут соответственно равны.
Следовательно, вероятность того, что объект поражен первым стрелком, равна 0,61.
Пример 2
Экономист полагает, что в течение периода активного экономического роста американский доллар будет расти в цене с вероятностью 0,7, в период умеренного экономического роста доллар подорожает с вероятностью 0,4, и при низких темпах экономического роста доллар подорожает с вероятностью 0,2.
В течение любого периода времени вероятность активного экономического роста равна 0,3, в периоды умеренного экономического роста — 0,5 и низкого роста — 0,2.
Предположим, доллар дорожает в течение текущего периода, чему равна вероятность того, что анализируемый период совпал с периодом активного экономического роста?
Решение. Обозначим гипотезы: $Н_1$ — «активный экономический рост»; $H_2$ — «умеренный экономический рост»; $H_3$ — «низкий экономический рост».
Обозначим событие А — «доллар дорожает». Получим:
$Р(Н_1) = 0,3$;
$Р(Н_2) = 0,5$;
$Р(Н_3) = 0,2$;
$Р(А/Н_1) = 0,7$;
$Р(А/Н_2) = 0,4$;
$Р(A/Н_3) = 0,2$.
Необходимо найти: $Р(Н_1/А)$.
Пользуясь формулой Бейеса и подставив заданные значения вероятностей, получаем:
[=frac{0,3cdot 0,7}{0,3cdot 0,7+0,5cdot 0,4+0,2cdot 0,2} =0,467.]
Пример 3
При разрыве бронебойного снаряда крупные осколки составляют 20% от общего числа осколков, средние — 30%, мелкие 50%. Вероятность того, что крупный осколок пробьет броню танка, равна 0,8. Для мелких и средних осколков эти вероятности соответственно равны 0,5 и 0,2.
- Найти вероятность того, что осколок пробьет броню.
- Броня танка оказалась пробитой. Найти вероятность того, что пробоина произошла от мелкого осколка.
Решение.
Обозначим события: $А$ — броня танка пробита; $H_1$ — осколок крупный; $H_2$ — осколок средний; $H_3$ — осколок мелкий.
https://www.youtube.com/watch?v=Z5zaBaX9qL0
События $H_1$, $H_2$, $H_3$ — это полная система гипотез. Найдем вероятности этих гипотез. По условию 20% осколков крупные, 30% — средние и 50% — мелкие. Найдем вероятности событий $H_1$, $H_2$, $H_3$:
$$P(H_1)=0,2;$$ $$P(H_2)=0,3;$$ $$P(H_3)=0,5.$$
Выполним проверку:
$$P(H_1)+P(H_2)+P(H_3)=0,2+0,3+0,5=1.$$
Найдем условные вероятности события А при наших гипотезах. Получим:
$$P(А /H_1)=0,8; P(А /H_2)=0,5; P(А /H_3)=0,2.$$
Вероятность события А посчитаем за формулой полной вероятности и получим:
Для решения второй части задачи воспользуемся формулой Байеса. Найдем вероятность того, что пробоина в броне произошла от мелкого осколка (событие $H_3$), т.е. вероятность $P(H_3/А)$. По формуле Байеса найдем значение:
Пример 4
Специализированая больница принимает в среднем 40% больных, которые имеют заболевание $H_1$, 35% — что имеют заболевание $H_2$ и 25% — $H_3$. Статистически известно, что лечение болезни $H_1$ равняется 0,9, для болезни $H_2$ и $H_3$ эти вероятности равняются 0,8 и 0,7. Какая вероятность того, что выписаный из больницы болел болезнью $H_2$?
Решение. Будем считать, что выписаный из больницы полностью здоров. По формуле полной вероятности найдем $P(A)$. По условию задачи:
$$Р(Н_1) = 0,4; $$ $$Р(Н_2) = 0,35;$$ $$Р(Н_3) = 0,25;$$$$Р(А/Н_1) = 0,9;$$ $$Р(А/Н_2) = 0,8$$ $$Р(A/Н_3) = 0,7. $$
Тогда по формуле полной вероятности:
По формуле Байеса найдем:
[=frac{0,35cdot 0,8}{0,815} =0,344.]
Видео:08 Формула полной вероятности ЗадачиСкачать

Реферат: Формула полной вероятности и формула Бейеса Байеса и их применение
Сибирский государственный университет телекоммуникаций и информатики
Кафедра высшей математики
РЕФЕРАТ
по дисциплине: «Теория вероятностей и математическая статистика»
на тему:
«Формула полной вероятности и формула Бейеса(Байеса) и их применение»
Выполнил:
Руководитель: профессор Б.П.Зеленцов
Новосибирск, 2010
Введение 3
1. Формула полной вероятности 4-5
2. Формула Байеса(Бейеса) 5-6
3. Задачи с решениями 7-11
4. Основные сферы применения формулы Байеса(Бейеса) 11
Заключение 12
Литература 13
Введение
Теория вероятностей является одним из классических разделов математики. Она имеет длительную историю. Основы этого раздела науки были заложены великими математиками. Назову, например, Ферма, Бернулли, Паскаля. Позднее развитие теории вероятностей определились в работах многих ученых.
Большой вклад в теорию вероятностей внесли ученые нашей страны:
П.Л.Чебышев, А.М.Ляпунов, А.А.Марков, А.Н.Колмогоров. Вероятностные и статистические методы в настоящее время глубоко проникли в приложения. Они используются в физике, технике, экономке, биологии и медицине.
Особенно возросла их роль в связи с развитием вычислительной техники.
Например, для изучения физических явлений производят наблюдения или опыты. Их результаты обычно регистрируют в виде значений некоторых наблюдаемых величин. При повторении опытов мы обнаруживаем разброс их результатов.
Например, повторяя измерения одной и той же величины одним и тем же прибором при сохранении определенных условий (температура, влажность и т.п.), мы получаем результаты, которые хоть немного, но все же отличаются друг от друга. Даже многократные измерения не дают возможности точно предсказать результат следующего измерения.
В этом смысле говорят, что результат измерения есть величина случайная. Еще более наглядным примером случайной величины может служить номер выигрышного билета в лотерее. Можно привести много других примеров случайных величин. Все же и в мире случайностей обнаруживаются определенные закономерности.
Математический аппарат для изучения таких закономерностей и дает теория вероятностей.
Таким образом, теория вероятностей занимается математическим анализом случайных событий и связанных с ними случайных величин.
1. Формула полной вероятности
Пусть имеется группа событий H 1 ,H 2 ,…, Hn, обладающая следующими свойствами:
1) все события попарно несовместны: HiHj =Æ; i, j =1,2,…,n; i¹j ;
2) их объединение образует пространство элементарных исходов W:
W = .
В этом случае будем говорить, что H 1, H 2 ,…,Hn образуют полную группу событий. Такие события иногда называют гипотезами .
https://www.youtube.com/watch?v=HQOuJ7xNTVc
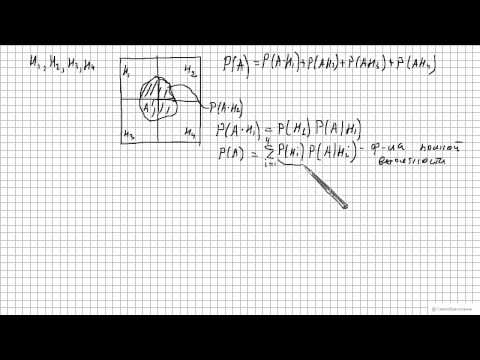
Пусть А – некоторое событие: А ÌW (диаграмма Венна представлена на рисунке 8). Тогда имеет место формула полной вероятности:
P (A ) = P (A /H 1 )P (H 1 ) + P (A /H 2 )P (H 2 ) + …+P (A /Hn )P (Hn ) =
Доказательство. Очевидно: A = , причем все события (i = 1,2,…,n ) попарно несовместны. Отсюда по теореме сложения вероятностей получаем
P (A ) = P () + P () +…+ P (
Если учесть, что по теореме умножения P () = P (A/H i )P (H i ) (i = 1,2,…,n ), то из последней формулы легко получить приведенную выше формулу полной вероятности.
Пример. В магазине продаются электролампы производства трех заводов, причем доля первого завода — 30%, второго — 50%, третьего — 20%. Брак в их продукции составляет соответственно 5%, 3% и 2%. Какова вероятность того, что случайно выбранная в магазине лампа оказалась бракованной.
Пусть событие H 1 состоит в том, что выбранная лампа произведена на первом заводе, H 2 на втором, H 3 — на третьем заводе. Очевидно:
P (H 1 ) = 3/10, P (H 2 ) = 5/10, P (H 3 ) = 2/10.
Пусть событиеА состоит в том, что выбранная лампа оказалась бракованной; A/Hi означает событие, состоящее в том, что выбрана бракованная лампа из ламп, произведенных на i -ом заводе. Из условия задачи следует:
P (A/H 1 ) = 5/10; P (A/H 2 ) = 3/10; P (A/H 3 ) = 2/10
По формуле полной вероятности получаем
2. Формула Байеса( Бейеса)
Пусть H 1 ,H 2 ,…,Hn — полная группа событий и А Ì W – некоторое событие. Тогда по формуле для условной вероятности
(1)
Здесь P (Hk /A ) – условная вероятность события (гипотезы) Hk или вероятность того, что Hk реализуется при условии, что событие А произошло.
По теореме умножения вероятностей числитель формулы (1) можно представить в виде
P = P = P (A /Hk )P (Hk )
Для представления знаменателя формулы (1) можно использовать формулу полной вероятности
P (A )
Теперь из (1) можно получить формулу, называемую формулой Байеса :
По формуле Байеса исчисляется вероятность реализации гипотезы Hk при условии, что событие А произошло. Формулу Байеса еще называют формулой вероятности гипотез. Вероятность P (Hk ) называют априорной вероятностью гипотезы Hk, а вероятность P (Hk /A ) – апостериорной вероятностью.
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.
Пример. Рассмотрим приведенную выше задачу об электролампах, только изменим вопрос задачи. Пусть покупатель купил электролампу в этом магазине, и она оказалась бракованной. Найти вероятность того, что эта лампа изготовлена на втором заводе.
Величина P (H 2 ) = 0,5 в данном случае это априорная вероятность события, состоящего в том, что купленная лампа изготовлена на втором заводе.
Получив информацию о том, что купленная лампа бракованная, мы можем поправить нашу оценку возможности изготовления этой лампы на втором заводе, вычислив апостериорную вероятность этого события.
Выпишем формулу Байеса для этого случая
Из этой формулы получаем: P (H 2 /A ) = 15/34. Как видно, полученная информация привела к тому, что вероятность интересующего нас события оказывается ниже априорной вероятности.
3. Задачи с решениями.
Задача 1. В магазин поступила новая продукция с трех предприятий.
Процентный состав этой продукции следующий: 20% — продукция первого предприятия, 30% — продукция второго предприятия, 50% — продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии — 5% и на третьем — 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.
Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
https://www.youtube.com/watch?v=938c02RDpI8
Можно применить формулу полной вероятности, причем в наших обозначениях:
Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:
Задача 2. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.
Решение. Возможны три гипотезы:
— на линию огня вызван первый стрелок,
— на линию огня вызван второй стрелок,
— на линию огня вызван третий стрелок.
Так как вызов на линию огня любого стрелка равновозможен, то
В результате опыта наблюдалось событие В — после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:
по формуле Байеса находим вероятность гипотезы после опыта:
Задача 3. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.
а) Каков процент брака на конвейере?
б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?
Решение. Возьмем с конвейера наудачу одну деталь и рассмотрим событие А – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: – взятая наудачу деталь обработана на -ом станке, .
Условные вероятности (в условии задачи они даны в форме процентов):
Зависимости между производительностями станков означают следующее:
.
А так как гипотезы образуют полную группу, то .
Решив полученную систему уравнений, найдем: .
а) Полная вероятность того, что взятая наудачу с конвейера деталь – бракованная:
.
Другими словами, в массе деталей, сходящих с конвейера, брак составляет 4%.
б) Пусть известно, что взятая наудачу деталь – бракованная. Пользуясь формулой Байеса, найдем условные вероятности гипотез:
,
,
.
Таким образом, в общей массе бракованных деталей на конвейере доля первого станка составляет 33%, второго – 39%, третьего – 28%.
Задача 4.
В первой урне 2 белых и 6 черных шаров, во второй – 4 белых и 2 черных. Из первой урны наудачу переложили 2 шара во вторую, после чего из второй урны наудачу достали один шар.
а) Какова вероятность того, что этот шар белый?
б) Шар, взятый из второй урны, оказался белым. Какова вероятность того, что из первой урны во вторую были переложены 2 белых шара?
Решение.
Введем обозначения:
А – шар, извлеченный из второй урны, белый;
гипотезы – из первой урны во вторую переложены 2 белых шара,
– переложены 2 разноцветных шара,
– переложены 2 черных шара.
Тогда
Вероятности гипотез и условие вероятности вычисляем по классической схеме:
Полученные результаты подставим в формулу полной вероятности:
б) Вероятность находим по формуле Байеса :
4. Основные сферы применения формулы Байеса(Бейеса)
1)Математический инструмент в теории вероятностей.
2)В статистике – как обобщение предшествующего опыта. Предполагается, что нами накоплен опыт, позволяющий экспериментально оценить априорное распределение вероятностей. Далее мы верим в то, что рассматриваемый нами новый объект относится к той же группе. Это позволяет строить классификаторы, основанные на байесовской формуле.
3)В статистике — для сравнения разных моделей в случае, когда априорные распределения настолько нечетки, что вообще несущественны. Очень часто используется BIC (байесовский информационный критерий).
4)Описание умонастроения. Сторонники интерпретации вероятности события как меры субъективной уверенности в его возможности могут пересчитывать эти величины в процессе появления новых данных. Очевидно, что математика здесь может быть подобной мельнице перемалывающей труху: произвол в определении априорных вероятностей может быть опасным.
Заключение
Формула полной вероятности широко использовалась математиками при конкретных расчётах ещё в начале XVIII века, но впервые была сформулирована как одно из основных утверждений теории вероятностей Пьером-Симоном Лапласом лишь в конце того века. Она применяется, в частности, при нахождении среднего выходного уровня дефектности в задачах статистического обеспечения качества продукции.
https://www.youtube.com/watch?v=MeGO4DLuvKY
Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной.
События, отражающие действие «причин», в данном случае обычно называют гипотезами, так как они — предполагаемые события, повлекшие данное.
Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще ), а условную — с учетом факта произошедшего события — апостериорной (насколько вероятна причина оказалась с учетом данных о событии ).
Можно также уточнять вероятность гипотезы, учитывая другие имеющиеся данные (другие произошедшие события). Для учета каждого следующего события нужно в качестве априорной вероятности гипотезы подставлять ее апостериорную вероятность с предыдущего шага.
Литература
1. Вентцель Е.С. Теория вероятностей. — М, «Высшая школа» 2002
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. — М, «Высшая школа» 2004
3. Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике. – М, «Айрис-пресс» 2004 г.
4. Сайт: Численные методы и теория вероятностей. www.uchites.ru/
5. Гмурман В. Е. Теория вероятностей и математическая статистика, — М.: Высшее образование.2005.
Видео:Теория вероятностей #11: формула полной вероятности, формула БайесаСкачать

Формула полной вероятности. Формулы Бейеса. Примеры решения задач
Как известно, вероятностью события А называют отношение числа m исходов испытаний, благоприятствующих наступлению события А, к общему числу n всех равновозможных несовместных исходов: Р(А)=m/n.
Кроме того, условной вероятностью события А (вероятностью события А при условии, что наступило событие В) называется число РВ(А) = Р(АВ)/Р(В), где А и В – два случайных события одного и того же испытания.
Поскольку события представимы в виде суммы и произведения, то и существуют правила сложения вероятностей событий и, соответственно, правила умножения вероятностей. Теперь дадим понятие полной вероятности.
Предположим, что событие А может наступить только вместе с одним из попарно несовместных событий Н1, Н2, Н3, …, Нn, называемых гипотезами. Тогда справедлива следующая формула полной вероятности:
Р(А) = Р(Н1)*РН1(А)+ Р(Н2)*РН2(А)+…+ Р(Нn)*РНn(А) = ∑Р(Нi) *РНi(А),
т.е. вероятность события А равна сумме произведений условных вероятностей этого события по каждой из гипотез на вероятность самих гипотез.
Если событие А уже произошло, то вероятности гипотез (априорные вероятности) могут быть переоценены (апостериорные вероятности) по формулам Бейеса:
Примеры решения задач по теме «Формула полной вероятности. Формулы Бейеса»
Задача 1.
На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 3% брака, второй – 2% и третий – 4%. Найти вероятность того, что на сборку попадает бракованная деталь, если с первого автомата поступает 100 деталей, со второго – 200 и с третьего – 250 деталей.
Решение. 1. Рассматриваем следующие события и гипотезы:
- событие А = {на сборку попадает бракованная деталь};
- гипотеза Н1 = {эта деталь с первого автомата}, Р(Н1)= 100/(100+200+250) =100/550=2/11;
- гипотеза Н2 = {эта деталь со второго автомата}, Р(Н2)= 200/(100+200+250) = 200/550=4/11;
- гипотеза Н3 = {эта деталь с третьего автомата}, Р(Н3)= 250/(100+200+250) = 250/550=5/11.
2. Условные вероятности того, что деталь бракованная составляют РН1(А)=3%=0,03, РН2(А)=2%=0,02, РН3(А)=4%=0,04.
3. По формуле полной вероятности находим
Р(А)= Р(Н1)*РН1(А)+ Р(Н2)*РН2(А)+Р(Н3)*РН3(А) = 0,03*2/11 + 0,02*4/11 + 0,04*5/11 = 34/1100 ≈ 0,03
Задача 2.
Имеются две одинаковые урны. Первая содержит 2 черных и 3 белых шара, вторая – 2 черных и 1 белый шар. Сначала произвольно выбирают урну, а затем из нее наугад извлекают один шар. Какова вероятность того, что будет выбран белый шар?
Решение. 1. Рассматриваем следующие события и гипотезы:
- А = {белый шар извлечен из произвольной урны};
- Н1 = {шар принадлежит первой урне}, Р(Н1)=1/2=0,5;
- Н2 = {шар принадлежит второй урне}, Р(Н2)=1/2=0,5;
2. Условная вероятность того, что белый шар принадлежит первой урне РН1(А)=3/(2+3)=3/5, а условная вероятность того, что белый шар принадлежит второй урне РН2(А)=1/(2+1)=1/3;
3. По формуле полной вероятности получим Р(А) = Р(Н1)*РН1(А)+Р(Н2)*РН2(А) = 0,5*3/5 + 0,5*1/3 = 3/10 + 1/6 = 7/15 ≈ 0,47
Задача 3.
Литье в болванках поступает из двух заготовительных цехов: из первого цеха – 70%, из второго цеха 30%. Литье первого цеха имеет 10% брака, литье из второго – 20% брака. Взятая наудачу болванка оказалась без дефекта. Какова вероятность ее изготовления первым цехом?
Решение. 1. Рассматриваем следующие события и гипотезы:
- событие А = {болванка без дефекта};
- гипотеза Н1 = {болванка изготовлена первым цехом}, Р(Н1)=70%=0,7;
- гипотеза Н2 = {болванка изготовлена вторым цехом}, Р(Н2)=30%=0,3.
2. Так как литье первого цеха имеет 10% брака, то 90% болванок, изготовленных первым цехом, не имеют дефекта, т.е. РН1(А)=0,9.
Литье второго цеха имеет 20% брака, то 80% болванок, изготовленных вторым цехом, не имеют дефекта, т.е. РН2(А)=0,8.
3. По формулу Бейеса найдем РА(Н1)
= 0,7*0,9/(0,7*0,9+0,3*0,8)= 0,63/0,87≈0,724.
Другие статьи по данной теме:
Список использованных источников
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / М. — «Высшая школа», 2004;
- Лисьев В.П. Теория вероятностей и математическая статистика: Учебное пособие/ Московский государственный университет экономики, статистики и информатики. – М., 2006;
- Семёнычев В. К. Теория вероятности и математическая статистика: Лекции /Самара, 2007;
- Теория вероятностей: контрольные работы и метод. указания для студентов / сост. Л.В. Рудная и др. / УрГЭУ — Екатеринбург, 2008.
Видео:Формула Байеса. Какова вероятность болезни?Скачать

Как применять теорему Байеса для решения реальных задач
Возможно, вы никогда не слышали про теорему Байеса, но пользовались ей постоянно. Например, изначально вы оценили вероятность получения прибавки к зарплате как 50%.
Получив положительные отзывы от менеджера, вы скорректировали оценку в лучшую сторону, и, наоборот, уменьшили ее, если сломали кофемашину на работе.
Так происходит уточнение значения вероятности по мере аккумулирования информации.
Основная идея теоремы Байеса состоит в том, чтобы получить большую точность оценки вероятности события путем учета дополнительных данных.
Принцип прост: есть первоначальная оценка вероятности, которую уточняют c получением большего количества информации.
Формула Байеса
Интуитивные действия формализуются в простом, но мощном уравнении (формула вероятности Байеса):
Левая часть уравнения — апостериорная (полученная в результате опыта) оценка вероятности события А при условии наступления события В (условная вероятность).
- P(A) — вероятность события А (основная, априорная оценка);
- P(B|A) — вероятность (также условная), которую мы получаем из наших данных;
- а P(B) — константа нормировки, которая ограничивает вероятность значением 1.
Это короткое уравнение является основой байесовского метода.
Абстрактность событий А и В не позволяет четко осознать смысл этой формулы. Для понимания сути теоремы Байеса рассмотрим реальную задачу.
Пример
Одной из тем, над которой я работаю, является изучение моделей сна. У меня есть данные за два месяца, записанные с помощью моих часов Garmin Vivosmart, показывающие, во сколько я засыпаю и просыпаюсь. Окончательная модель, показывающая наиболее вероятное распределение вероятности сна как функцию времени (MCMC — приблизительный метод), приведена ниже.
https://www.youtube.com/watch?v=M56eTPqDK88
Распределение вероятности сна
На графике приведена вероятность того, что я сплю, в зависимости лишь от времени. Как она изменится, если учесть время, в течение которого включен свет в спальне? Для уточнения оценки и нужна теорема Байеса. Уточненная оценка основана на априорной и имеет вид:
Выражение слева — вероятность того, что я сплю, при условии, что известно, включен ли свет в моей спальне. Априорная оценка в данный момент времени (приведена на графике выше) обозначена как P(sleep). Например, в 10:00 вечера априорная вероятность того, что я сплю, равна 27,34%.
Добавим больше информации, используя вероятность P(bedroom light|sleep), полученную из наблюдаемых данных.
Из собственных наблюдений мне известно следующее: вероятность того, что я сплю, когда свет включен, равна 1%.
Вероятность того, что свет выключен во время сна, равна 1-0,01 = 0,99 (знак «-» в формуле означает противоположное событие), потому что сумма вероятностей противоположных событий равна 1. Когда я сплю, то свет в спальне либо включен, либо выключен.
Наконец, уравнение также включает в себя константу нормировки P(light) — вероятность того, что свет включен. Свет бывает включен и когда я сплю, и когда бодрствую. Поэтому, зная априорную вероятность сна, вычислим константу нормировки так:
Вероятность того, что свет включен, учтена в обоих вариантах: либо я сплю, либо нет (P (-sleep) = 1 — P (sleep) — это вероятность того, что я не сплю.)
Вероятность того, что свет включен в тот момент, когда я не сплю, равна P(light|-sleep), и определяется путем наблюдения. Мне известно, что свет горит, когда я бодрствую, с вероятностью 80% (это означает, что есть 20% вероятность того, что свет не включен, если я бодрствую).
Окончательное уравнение Байеса принимает вид:
Оно позволяет вычислить вероятность того, что я сплю, при условии, что свет включен. Если нас интересует вероятность того, что свет выключен, нужно каждую конструкцию P(light|… заменить на P(-light|….
Давайте посмотрим, как используют полученные символьные уравнения на практике.
Применим формулу к моменту времени 22:30 и учтем, что свет включен. Мы знаем, вероятность того, что я спал, равна 73,90%. Это число — отправная точка для нашей оценки.
Уточним его, учтя информацию об освещении. Зная, что свет включен, подставим числа в формулу Байеса:
Дополнительные данные резко изменили оценку вероятности: от более 70% до 3,42%. Это показывает силу теоремы Байеса: мы смогли уточнить нашу первоначальную оценку ситуации, включив в нее больше информации. Возможно, мы уже интуитивно делали это раньше, но теперь, рассуждая об этом в терминах формальных уравнений, мы смогли подтвердить наши прогнозы.
Python
Рассмотрим еще один пример. Что если на часах 21:45 и свет выключен? Попытайте рассчитать вероятность самостоятельно, считая априорную оценку равной 0.1206.
Вместо того, чтобы каждый раз считать вручную, я написал простой код на Python для выполнения этих вычислений, который вы можете попробовать в Jupyter Notebook. Вы получите следующий ответ:
Time: 09:45:00 PM Light is OFF.
The prior probability of sleep: 12.06%
The updated probability of sleep: 40.44%
И снова дополнительная информация меняет нашу оценку. Теперь, если моя сестра захочет позвонить мне в 21:45 зная, что мой свет включен, она может воспользоваться этим уравнением, чтобы определить, смогу ли я взять трубку (предполагая, что я беру трубку только бодрствующим)! Кто говорит, что статистика неприменима повседневной жизни?
Визуализация вероятности
Наблюдение за вычислениями полезно, но визуализация помогает добиться более глубокого понимания результата. Я всегда стараюсь использовать графики, чтобы генерировать идеи, если они сами не приходят при простом изучении уравнений. Мы можем визуализировать априорное и апостериорное распределение вероятности сна с использованием дополнительных данных:
Когда свет включен, график смещается вправо, указывая на то, что я с меньшей вероятностью сплю в данный момент времени. Аналогично, график смещается влево, если мой свет выключен. Понять смысл теоремы Байеса непросто, но эта иллюстрация наглядно демонстрирует, зачем ее нужно использовать. Формула Байеса — инструмент для уточнения прогнозов с помощью дополнительных данных.
Что, если есть еще больше данных?
Зачем останавливаться на освещении в спальне? Мы можем использовать еще больше данных в нашей модели для дальнейшего уточнения оценки (пока данные остаются полезными для рассматриваемого случая). Например, я знаю, что если мой телефон заряжается, то я сплю с вероятностью 95%. Этот факт можно учесть в нашей модели.
Предположим, что вероятность того, что мой телефон заряжается, не зависит от освещения в спальне (независимость событий — это достаточно сильное упрощение, но оно позволит сильно облегчить задачу). Составим новое, еще более точное выражение для вероятности:
Получившаяся формула выглядит громоздко, но, используя код на Python, мы можем написать функцию, которая будет производить расчет. Для любого момента времени и любой комбинации наличия освещения/зарядки телефона эта функция возвращает уточненную вероятность того, что я сплю.
https://www.youtube.com/watch?v=V16KANPLD9o
Пропустим математику (все равно считать будет компьютер) и перейдем к результатам:
Time is 11:00:00 PM Light is ON Phone IS NOT charging.
The prior probability of sleep: 95.52%
The updated probability of sleep: 1.74%
В 23:00 без дополнительной информации мы могли почти с полной вероятностью сказать, что я сплю. Однако, как только у нас будет дополнительная информация о том, что свет включен, а телефон не заряжается, мы заключаем, что вероятность того, что я сплю, практически равна нулю. Вот еще один пример:
Time is 10:15:00 PM Light is OFF Phone IS charging.
The prior probability of sleep: 50.79%
The updated probability of sleep: 95.10%
Вероятность смещается вниз или вверх в зависимости от конкретной ситуации. Чтобы продемонстрировать это, рассмотрим четыре конфигурации дополнительных данных и то, как они изменяют распределение вероятности:
На этом графике представлено много информации, но главный смысл состоит в том, что кривая вероятности изменяется в зависимости от дополнительных факторов. По мере добавления других данных мы будем получать более точную оценку.
Заключение
Теорема Байеса и другие статистические понятия могут быть трудными для понимания, когда они представлены абстрактными уравнениями, использующими только буквы или выдуманные ситуации. Настоящее обучение приходит, когда мы применяем абстрактные понятия в реальных задачах.
Успех в области data science — это непрерывное обучение, добавление новых методов в набор навыков и поиск оптимального метода для решения задач.
Теорема Байеса позволяет уточнять наши оценки вероятности с помощью дополнительной информации для более качественного моделирования реальности.
Увеличение количества информации позволяет получать более точные прогнозы, и метод Байеса оказывается полезным инструментом для решения этой задачи.
Я приветствую обратную связь, дискуссию и конструктивную критику. Связаться со мной можно в : @koehrsen_will.
Может быть интересно:
Видео:Найти вероятность по формуле Байеса (Бейеса)Скачать

Формула полной вероятности и формула Бейеса Байеса и их применение
Сохрани ссылку в одной из сетей:
Сибирский государственныйуниверситет телекоммуникаций иинформатики
Кафедра высшей математики
РЕФЕРАТ
по дисциплине : «Теория вероятностейи математическая статистика»
на тему:
«Формула полной вероятности иформула Бейеса(Байеса) и их применение»
Выполнил:
Руководитель: профессорБ.П.Зеленцов
Новосибирск, 2010
Введение 3
Формула полной вероятности 4-5
Формула Байеса(Бейеса) 5-6
Задачи с решениями 7-11
Основные сферы применения формулы Байеса(Бейеса) 11
Заключение 12
Литература 13
Введение
Теория вероятностей являетсяодним из классических разделов математики.Она имеет длительную историю. Основыэтого раздела науки были заложенывеликими математиками. Назову, например,Ферма, Бернулли, Паскаля.Позднееразвитие теории вероятностей определилисьв работах многих ученых.
Большой вкладв теорию вероятностей внесли ученыенашей страны:
П.Л.Чебышев, А.М.Ляпунов,А.А.Марков, А.Н.Колмогоров. Вероятностныеи статистические методы в настоящеевремя глубоко проникли в приложения.Они используются в физике, технике,экономке, биологии и медицине.
Особенновозросла их роль в связи с развитиемвычислительной техники.
Например, для изучения физическихявлений производят наблюдения илиопыты. Их результаты обычно регистрируютв виде значений некоторых наблюдаемыхвеличин. При повторении опытов мыобнаруживаем разброс их результатов.
Например, повторяя измерения одной итой же величины одним и тем же приборомпри сохранении определенных условий(температура, влажность и т.п.), мы получаемрезультаты, которые хоть немного, новсе же отличаются друг от друга. Дажемногократные измерения не дают возможноститочно предсказать результат следующегоизмерения.
В этом смысле говорят, чторезультат измерения есть величинаслучайная. Еще более наглядным примеромслучайной величины может служить номервыигрышного билета в лотерее. Можнопривести много других примеров случайныхвеличин. Все же и в мире случайностейобнаруживаются определенные закономерности.
https://www.youtube.com/watch?v=iqkI3zpOhJU
Математический аппарат для изучениятаких закономерностей и дает теориявероятностей.
Таким образом, теориявероятностей занимается математическиманализом случайных событий и связанныхс ними случайных величин.
1. Формулаполной вероятности
Пусть имеется группасобытий H1,H2,…,Hn,обладающая следующими свойствами:
1) все события попарнонесовместны: HiHj=; i,j=1,2,…,n;ij;
2) их объединениеобразует пространство элементарныхисходов :
= .
Рис.8
В этом случае будем говорить,что H1, H2,…,Hn образуют полнуюгруппу событий. Такиесобытия иногда называют гипотезами.
Пусть А –некоторое событие: А (диаграмма Венна представлена на рисунке8). Тогда имеет место формулаполной вероятности:
P(A)= P(A/H1)P(H1)+ P(A/H2)P(H2)+ …+P(A/Hn)P(Hn)=
Доказательство.Очевидно: A = ,причем все события (i =1,2,…,n)попарно несовместны. Отсюда по теоремесложения вероятностей получаем
P(A)= P()+ P()+…+ P(
Если учесть, что потеореме умножения P() =P(A/Hi)P(Hi)(i = 1,2,…,n), то из последней формулы легко получитьприведенную выше формулу полнойвероятности.
Пример.В магазине продаются электролампыпроизводства трех заводов, причем доляпервого завода — 30,второго — 50,третьего — 20.Брак в их продукции составляетсоответственно 5,3и 2.Какова вероятность того, что случайновыбранная в магазине лампа оказаласьбракованной.
Пусть событие H1состоит в том, что выбранная лампапроизведена на первом заводе, H2на втором, H3- на третьем заводе. Очевидно:
P(H1)= 3/10, P(H2)= 5/10, P(H3)= 2/10.
Пусть событиеА состоит в том, чтовыбранная лампа оказалась бракованной;A/Hiозначает событие, состоящее в том, чтовыбрана бракованная лампа из ламп,произведенных на i-омзаводе. Из условия задачи следует:
P(A/H1)= 5/10; P(A/H2)= 3/10; P(A/H3)= 2/10
По формуле полной вероятностиполучаем
2. ФормулаБайеса( Бейеса)
Пусть H1,H2,…,Hn— полная группа событий и А – некоторое событие. Тогда по формуледля условной вероятности
(1)
Здесь P(Hk/A)– условная вероятность события (гипотезы)Hkили вероятность того, что Hkреализуется при условии, что событие Апроизошло.
По теореме умножениявероятностей числитель формулы (1) можнопредставить в виде
P= P=P(A/Hk)P(Hk)
Для представлениязнаменателя формулы (1) можно использоватьформулу полной вероятности
P(A)
Теперь из (1) можнополучить формулу, называемую формулойБайеса:
По формуле Байесаисчисляется вероятность реализациигипотезы Hkпри условии, что событие Апроизошло. Формулу Байеса еще называютформулой вероятностигипотез. ВероятностьP(Hk)называют априорной вероятностью гипотезыHk,а вероятность P(Hk/A)– апостериорной вероятностью.
Теорема.Вероятность гипотезыпосле испытания равна произведениювероятности гипотезы до испытания насоответствующую ей условную вероятностьсобытия, которое произошло при испытании,деленному на полную вероятность этогособытия.
Пример.Рассмотрим приведенную выше задачу обэлектролампах, только изменим вопросзадачи. Пусть покупатель купил электролампув этом магазине, и она оказаласьбракованной. Найти вероятность того,что эта лампа изготовлена на второмзаводе.
Величина P(H2)= 0,5 в данном случае это априорнаявероятность события, состоящего в том,что купленная лампа изготовлена навтором заводе.
Получив информацию отом, что купленная лампа бракованная,мы можем поправить нашу оценку возможностиизготовления этой лампы на второмзаводе, вычислив апостериорную вероятностьэтого события.
Выпишем формулу Байеса для этогослучая
https://www.youtube.com/watch?v=DaDQdqftavc
Из этой формулыполучаем: P(H2/A)= 15/34. Как видно, полученная информацияпривела к тому, что вероятностьинтересующего нас события оказываетсяниже априорной вероятности.
3. Задачи срешениями.
Задача 1. В магазинпоступила новая продукция с трехпредприятий.
Процентный состав этойпродукции следующий: 20% — продукцияпервого предприятия, 30% — продукциявторого предприятия, 50% — продукциятретьего предприятия; далее, 10% продукциипервого предприятия высшего сорта, навтором предприятии — 5% и на третьем — 20%продукции высшего сорта. Найти вероятностьтого, что случайно купленная новаяпродукция окажется высшего сорта.
Решение. Обозначимчерез В событие,заключающееся в том, что будет купленапродукция высшего сорта, через обозначимсобытия, заключающиеся в покупкепродукции, принадлежащей соответственнопервому, второму и третьему предприятиям.
https://www.youtube.com/watch?v=938c02RDpI8
Можно применить формулу полнойвероятности, причем в наших обозначениях:
Подставляя эти значения в формулуполной вероятности, получим искомуювероятность:
Задача 2. Один изтрех стрелков вызывается на линию огняи производит два выстрела. Вероятностьпопадания в мишень при одном выстреледля первого стрелка равна 0,3, для второго- 0,5; для третьего — 0,8. Мишень не поражена.Найти вероятность того, что выстрелыпроизведены первым стрелком.
Решение. Возможнытри гипотезы:
-на линию огня вызван первый стрелок,
-на линию огня вызван второй стрелок,
-на линию огня вызван третий стрелок.
Так как вызов на линию огня любогострелка равновозможен, то
В результате опыта наблюдалосьсобытие В — после произведенных выстреловмишень не поражена. Условные вероятностиэтого события при сделанных гипотезахравны:
по формуле Байеса находимвероятность гипотезы послеопыта:
Задача 3. На трехстанках-автоматах обрабатываютсяоднотипные детали, поступающие послеобработки на общий конвейер. Первыйстанок дает 2% брака, второй – 7%, третий– 10%. Производительность первого станкав 3 раза больше производительностивторого, а третьего – в 2 раза меньше,чем второго.
а) Каков процент брака на конвейере?
б) Каковы доли деталей каждогостанка среди бракованных деталей наконвейере?
Решение. Возьмемс конвейера наудачу одну деталь ирассмотрим событие А – деталь бракованная.Оно связано с гипотезами относительнотого, где была обработана эта деталь:–взятая наудачу деталь обработана на-омстанке, .
Условные вероятности (в условиизадачи они даны в форме процентов):
Зависимости между производительностямистанков означают следующее:
.
А так как гипотезы образуютполную группу, то .
Решив полученную системууравнений, найдем: .
а) Полная вероятность того, чтовзятая наудачу с конвейера деталь –бракованная:
.
Другими словами, в массе деталей,сходящих с конвейера, брак составляет4%.
б) Пусть известно, что взятаянаудачу деталь – бракованная. Пользуясьформулой Байеса, найдем условныевероятности гипотез:
,
,
.
Таким образом, в общей массебракованных деталей на конвейере доляпервого станка составляет 33%, второго– 39%, третьего – 28%.
Задача 4.
В первой урне 2 белых и 6 черныхшаров, во второй – 4 белых и 2 черных. Изпервой урны наудачу переложили 2 шараво вторую, после чего из второй урнынаудачу достали один шар.
а) Какова вероятность того, чтоэтот шар белый?
б) Шар, взятый из второй урны,оказался белым. Какова вероятностьтого, что из первой урны во вторую былипереложены 2 белых шара?
Решение.
Введем обозначения:
А – шар, извлеченныйиз второй урны, белый;
гипотезы –из первой урны во вторую переложены 2белых шара,
–переложены 2 разноцветных шара,
–переложены 2 черных шара.
Тогда
Вероятности гипотез иусловие вероятности вычисляемпо классической схеме:
Полученные результаты подставимв формулу полной вероятности:
б) Вероятность находимпо формуле Байеса:
4.Основные сферы применения формулыБайеса(Бейеса)
1)Математический инструмент втеории вероятностей.
2)В статистике – как обобщениепредшествующего опыта. Предполагается,что нами накоплен опыт, позволяющийэкспериментально оценить априорноераспределение вероятностей. Далее мыверим в то, что рассматриваемый наминовый объект относится к той же группе.Это позволяет строить классификаторы,основанные на байесовской формуле.
3)В статистике — для сравненияразных моделей в случае, когда априорныераспределения настолько нечетки, чтовообще несущественны. Очень частоиспользуется BIC (байесовский информационныйкритерий).
4)Описание умонастроения.Сторонники интерпретации вероятностисобытия как меры субъективной уверенностив его возможности могут пересчитыватьэти величины в процессе появления новыхданных. Очевидно, что математика здесьможет быть подобной мельнице перемалывающейтруху: произвол в определении априорныхвероятностей может быть опасным.
Заключение
Формулаполной вероятности широко использовалась математикамипри конкретных расчётах ещё в началеXVIII века, но впервые была сформулированакак одно из основных утверждений теориивероятностей Пьером-СимономЛапласомлишь в конце того века. Она применяется,в частности, при нахождении среднеговыходного уровня дефектности в задачахстатистического обеспечения качествапродукции.
https://www.youtube.com/watch?v=f7x0C7na-is
Формула Байеса позволяет«переставить причину и следствие»: поизвестному факту события вычислитьвероятность того, что оно было вызваноданной причиной.
События, отражающие действие«причин», в данном случае обычно называютгипотезами,так как они — предполагаемыесобытия, повлекшие данное.
Безусловнуювероятность справедливости гипотезыназывают априорной(насколько вероятна причина вообще),а условную — с учетом факта произошедшегособытия — апостериорной(насколько вероятна причина оказаласьс учетом данных о событии).
Можно также уточнять вероятностьгипотезы, учитывая другие имеющиесяданные (другие произошедшие события).Для учета каждого следующего событиянужно в качестве априорной вероятностигипотезы подставлять ее апостериорнуювероятность с предыдущего шага.
Литература
Вентцель Е.С. Теория вероятностей. — М, «Высшая школа» 2002
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. — М, «Высшая школа» 2004
Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике. – М, «Айрис-пресс» 2004 г.
Сайт: Численные методы и теория вероятностей. http://www.uchites.ru/
Гмурман В. Е. Теория вероятностей и математическая статистика, — М.: Высшее образование.2005.
🔥 Видео
Формула полной вероятности. Формула БайесаСкачать

✓ Формула Байеса в реальной жизни | Математика вокруг нас | Борис ТрушинСкачать

Формула полной вероятности. Формула Байеса.Скачать

Решение задач по теории вероятностей | Часть 2 | Формула полной вероятности и формула БайесаСкачать

Математика без Ху!ни. Сложение и умножение вероятностей. Формула полной вероятности.Скачать

Формула полной вероятности. Формула БайесаСкачать
Формула полной вероятности.Скачать

Решение задач на тему "Формула полной вероятности. Формула Байеса"Скачать

✓ Условная вероятность и формула Байеса. Задача про два кубика | Ботай со мной #106 | Борис ТрушинСкачать

Теория вероятностей #8: формула Бернулли и примеры ее использования при решении задачСкачать

Решение задач по теме: "Формула полной вероятности и формула Байеса" (с тайм-кодами).Скачать

Формула полной вероятности на конкретных примерах. №5 ЕГЭ профильСкачать

ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛЫ БАЙЕСАСкачать

Математика без Ху!ни. Теория вероятностей. Схема БернуллиСкачать

Условная вероятность.Формула БайесаСкачать

#15. Формула Байеса при решении конкретных задач | Машинное обучениеСкачать