📊 Распределения вероятностей для непрерывных случайных величин

Приветствую вас, дорогие слушатели! Сегодня мы поговорим о том, как описывать и анализировать непрерывные случайные величины с помощью распределений вероятностей. Непрерывные случайные величины — это такие величины, которые могут принимать любые значения из некоторого интервала числовой оси. Например, время ожидания автобуса, длина телефонного разговора, температура воздуха и т.д. Для таких величин мы не можем перечислить все возможные исходы, как для дискретных случайных величин, поэтому нам нужен другой способ задания их закона распределения. 🤔

Для непрерывных случайных величин мы используем понятие функции плотности вероятности, которая показывает, насколько вероятно, что случайная величина примет значение, близкое к данному. Функция плотности вероятности обладает следующими свойствами: 😊

• Она неотрицательна, то есть f(x) ≥ 0 для любого x;
• Она интегрируема, то есть существует определенный интеграл ∫f(x)dx по всей области значений случайной величины;
• Она нормирована, то есть ее интеграл равен единице: ∫f(x)dx = 1;
• Она определяет вероятность попадания случайной величины в любой интервал (a;b) по формуле Р(a < X < b) = ∫f(x)dx, где интеграл берется от a до b.

Кроме функции плотности вероятности, для непрерывных случайных величин также вводится понятие функции распределения, которая показывает, какая доля значений случайной величины не превосходит данное число. Функция распределения обозначается буквой F и вычисляется по формуле F(x) = Р(X ≤ x) = ∫f(t)dt, где интеграл берется от минус бесконечности до x. Функция распределения обладает следующими свойствами: 😊

• Она неубывающая, то есть если x1 < x2, то F(x1) ≤ F(x2);
• Она непрерывная, то есть не имеет скачков;
• Она ограниченная, то есть 0 ≤ F(x) ≤ 1 для любого x;
• Она стремится к нулю при x → -∞ и к единице при x → +∞, то есть F(-∞) = 0 и F(+∞) = 1;
• Она определяет вероятность попадания случайной величины в любой интервал (a;b) по формуле Р(a < X < b) = F(b) — F(a).

Зная функцию плотности или функцию распределения непрерывной случайной величины, мы можем найти ее числовые характеристики, такие как математическое ожидание, дисперсия, среднее квадратическое отклонение и т.д. Эти характеристики позволяют оценить среднее значение, разброс, асимметрию и эксцесс случайной величины. Для нахождения этих характеристик мы используем определенные интегралы от функции плотности или функции распределения. 😊

Существует много разных видов распределений вероятностей для непрерывных случайных величин, которые описывают различные явления в природе, науке, технике, экономике и т.д. Некоторые из них мы рассмотрим подробнее в этой лекции. Это: 😍

• Равномерное распределение;
• Показательное распределение;
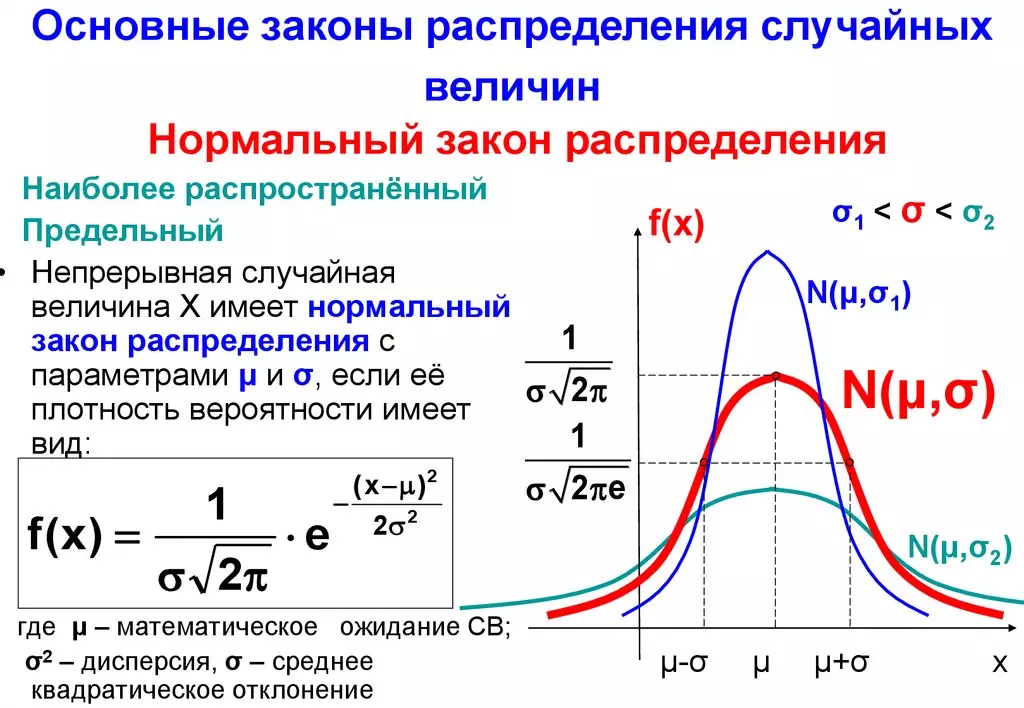
• Нормальное распределение.

Видео:Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать

📈 Равномерное распределение

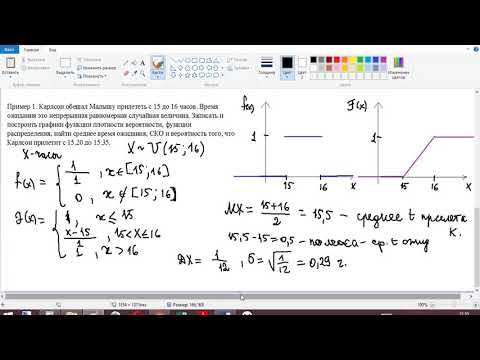
Равномерным распределением называется распределение вероятностей непрерывной случайной величины X, которая принимает значения на отрезке [a;b] с постоянной плотностью. Это означает, что вероятность попадания случайной величины в любой подотрезок одинакова и пропорциональна его длине. Например, если X — время ожидания автобуса, который ходит строго по расписанию с интервалом 10 минут, то X имеет равномерное распределение на отрезке [0;10]. 😊

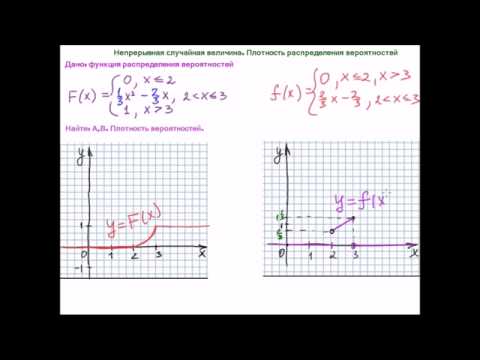
Функция плотности вероятности для равномерного распределения имеет вид:

Функция распределения для равномерного распределения имеет вид:

F(x)={0,если xb.F(x) = begin{cases}
0, & text{если } x < a, \
frac{x-a}{b-a}, & text{если } a le x le b, \
1, & text{если } x > b.
end{cases}F(x)=⎩⎨⎧​0,b−ax−a​,1,​если xb.​

Математическое ожидание для равномерного распределения равно среднему арифметическому границ отрезка:

Дисперсия для равномерного распределения равна квадрату четверти длины отрезка, деленному на три:

Среднее квадратическое отклонение для равномерного распределения равно длине отрезка, деленной на два корня из трех:

Пример. Пусть X — время ожидания автобуса, который ходит строго по расписанию с интервалом 10 минут. Тогда X имеет равномерное распределение на отрезке [0;10]. Найдем вероятность того, что пассажир будет ждать автобус не более 3 минут и не менее 7 минут. 😊

Решение. Вероятность того, что пассажир будет ждать автобус не более 3 минут, рав на три минуты, равна отношению длины подотрезка [0;3] к длине отрезка [0;10], то есть Р(X ≤ 3) = F(3) = 3/10 = 0.3. Вероятность того, что пассажир будет ждать автобус не менее 7 минут, равна отношению длины подотрезка [7;10] к длине отрезка [0;10], то есть Р(X ≥ 7) = 1 — F(7) = 1 — 7/10 = 0.3. Вероятность того, что пассажир будет ждать автобус не более 3 минут или не менее 7 минут, равна сумме этих вероятностей, то есть Р(X ≤ 3 или X ≥ 7) = Р(X ≤ 3) + Р(X ≥ 7) = 0.3 + 0.3 = 0.6. 😊

Видео:Теория вероятностей #12: случайная величина, плотность и функция распределенияСкачать

📉 Показательное распределение

Показательным распределением называется распределение вероятностей непрерывной случайной величины X, которая принимает неотрицательные значения с убывающей плотностью. Это означает, что вероятность того, что случайная величина примет большое значение, меньше, чем вероятность того, что она примет маленькое значение. Например, если X — время до поломки некоторого прибора, который подвержен износу, то X имеет показательное распределение. 😊

Функция плотности вероятности для показательного распределения имеет вид:

Здесь параметр λ > 0 называется интенсивностью и характеризует скорость убывания плотности. Чем больше λ, тем быстрее падает вероятность больших значений случайной величины.

Функция распределения для показательного распределения имеет вид:

Математическое ожидание для показательного распределения равно обратному значению интенсивности:

Дисперсия для показательного распределения равна квадрату обратного значения интенсивности:

Среднее квадратическое отклонение для показательного распределения равно обратному значению интенсивности:

📸 Видео

Функция распределения непрерывной случайной величины. Вероятность попадания в интервалСкачать

Нормальное Распределение за 6 МинутСкачать

Законы распределения непрерывных случайных величинСкачать

Экспоненциальное (показательное) распределение непрерывной случайной величины.Скачать

Теория вероятностей #18: системы двух случайных величин, двумерное распределениеСкачать

Функция распределения и плотность распределенияСкачать

Функция распределения дискретной случайной величиныСкачать

Непрерывная случайная величина. Функция распределенияСкачать

Теория вероятностей #19: ковариация, корреляция, зависимость двух случайных величинСкачать

2.2. Функция распределения и ее характеристики.Скачать

Непрерывная случайная величина. Плотность вероятностейСкачать

Непрерывная случайная величина и ее свойстваСкачать

Равномерное распределение случайной величиныСкачать

Равномерное распределение непрерывной случайной величины.Скачать

Биноминальное распределениеСкачать

Непрерывные случайные величины Плотность вероятностиСкачать

14 Непрерывные случайные величины ЗадачиСкачать

Непрерывные случайные величиныСкачать