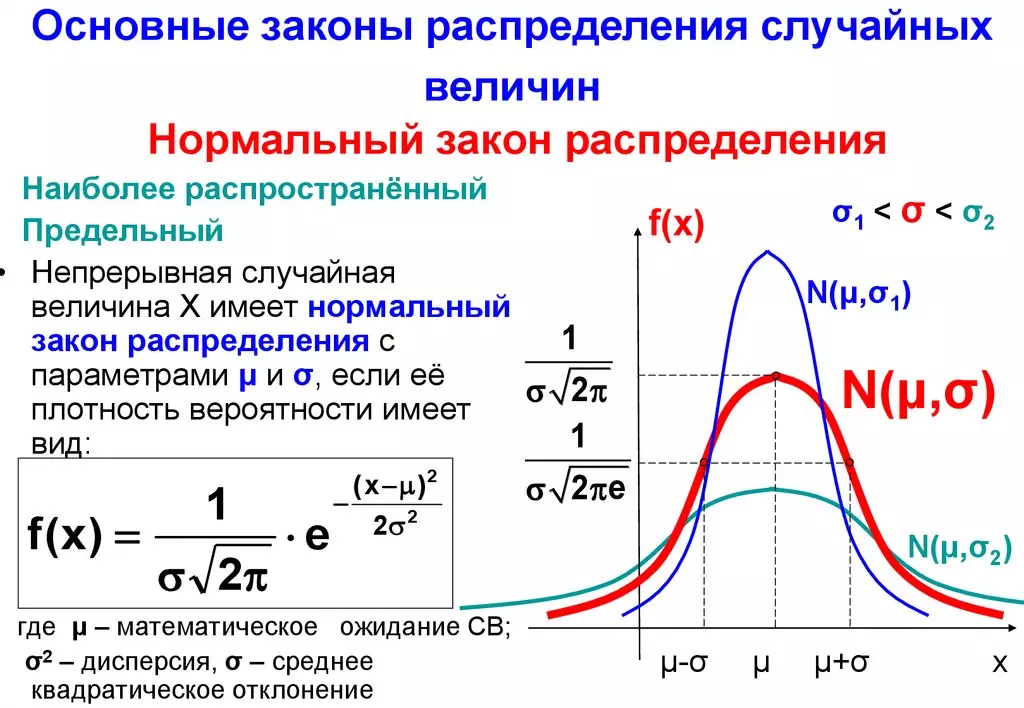
📚 Нормальное распределение непрерывной случайной величины (3 видео)

Нормальное распределение является одним из самых важных и часто используемых в статистике типов распределения вероятностей для непрерывной случайной величины. Его график имеет форму колокола и симметричен относительно среднего значения. 😮

Нормальное распределение описывает множество явлений в природе, науке, технике, экономике и других областях. Например, рост, вес, давление, температура, скорость, IQ, доход и многое другое. 😯

Нормальное распределение также является основой для многих статистических методов, таких как доверительные интервалы, гипотезы, регрессия, анализ данных и машинное обучение. 😍

В этой лекции мы рассмотрим основные свойства, характеристики и применения нормального распределения. Мы также узнаем, как работать с нормальными случайными величинами, как находить их вероятности, математическое ожидание, дисперсию и стандартное отклонение. 😊

Содержание

🔎 Определение и обозначение нормального распределения
📈 График нормального распределения
📊 Стандартное нормальное распределение
📏 Правило трех сигм
📐 Нахождение вероятностей для нормального распределения
📺 Видео

Видео:Нормальное распределение непрерывной случайной величиныСкачать

🔎 Определение и обозначение нормального распределения

Нормальное распределение — это распределение вероятностей для непрерывной случайной величины X, которое определяется следующей функцией плотности вероятности: 😲

Здесь μmuμ — это математическое ожидание (среднее значение) X, а σsigmaσ — это стандартное отклонение X. Эти два параметра полностью определяют форму и положение нормального распределения. 😎

Нормальное распределение обозначается как X∼N(μ,σ2)X sim N(mu, sigma^2)X∼N(μ,σ2), где σ2sigma^2σ2 — это дисперсия X. Это означает, что случайная величина X имеет нормальное распределение с параметрами μmuμ и σ2sigma^2σ2. 😁

Видео:Теория вероятностей #12: случайная величина, плотность и функция распределенияСкачать

📈 График нормального распределения

График нормального распределения имеет форму колокола, который симметричен относительно вертикальной прямой x=μx = mux=μ. 😮

Высота колокола определяется значением функции плотности вероятности f(x)f(x)f(x) в данной точке. 😯

Ширина колокола зависит от значения стандартного отклонения σsigmaσ. Чем больше σsigmaσ, тем шире колокол и тем больше разброс значений случайной величины X. 😲

Площадь под графиком нормального распределения равна единице, то есть P(−∞<x<∞)=1p(-infty <="" x="" infty)="1P(−∞<X<∞)=1." 😍
</x

График нормального распределения также показывает, как распределены вероятности различных интервалов значений случайной величины X. Например, можно показать, что P(μ−σ<x<μ+σ)≈0.68p(mu -="" sigma="" <="" x="" mu="" +="" sigma)="" approx="" 0.68p(μ−σ<x<μ+σ)≈0.68,="" то="" есть="" вероятность="" того,="" что="" лежит="" в="" пределах="" одного="" стандартного="" отклонения="" от="" среднего,="" примерно="" равна="" 0.68.="" 😊
</x

Видео:Нормальное Распределение за 6 МинутСкачать

📊 Стандартное нормальное распределение

Стандартное нормальное распределение — это частный случай нормального распределения, когда μ=0mu = 0μ=0 и σ=1sigma = 1σ=1. 😮

Стандартное нормальное распределение обозначается как Z∼N(0,1)Z sim N(0, 1)Z∼N(0,1), где Z — это стандартизированная (или нормированная) случайная величина. 😎

Стандартизация — это процесс преобразования нормальной случайной величины X в стандартную нормальную случайную величину Z путем вычитания среднего и деления на стандартное отклонение: 😯

Стандартное нормальное распределение имеет ту же форму колокола, что и общее нормальное распределение, но симметрично относительно прямой x=0x = 0x=0. 😲

Стандартное нормальное распределение удобно использовать для нахождения вероятностей интервалов значений нормальной случайной величины X, так как для него существуют специальные таблицы и калькуляторы. 😍

Видео:Функция распределения непрерывной случайной величины. Вероятность попадания в интервалСкачать

📏 Правило трех сигм

Правило трех сигм — это эмпирическое правило, которое говорит, что для любой нормальной случайной величины X справедливы следующие приближенные равенства: 😮

Это означает, что большая часть значений случайной величины X сконцентрирована вокруг среднего значения μmuμ и лежит в пределах нескольких стандартных отклонений σsigmaσ. 😯

Правило трех сигм можно использовать для оценки вероятностей интервалов значений нормальной случайной величины X, когда нет доступа к таблицам или калькуляторам стандартного нормального распределения. 😊

Видео:Функция распределения и плотность распределенияСкачать

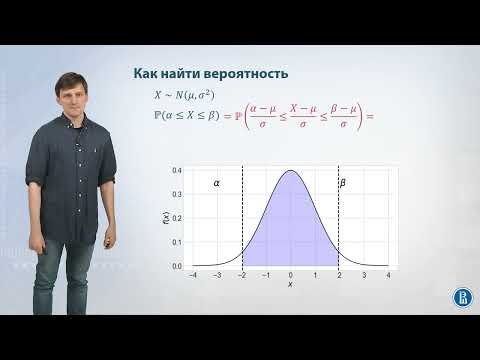
📐 Нахождение вероятностей для нормального распределения

Для нахождения вероятностей интервалов значений нормальной случайной величины X нужно выполнить следующие шаги: 😲

Стандартизировать интервал, то есть выразить его в терминах стандартной нормальной случайной в чиной Z. 😁
1. Стандартизировать интервал, то есть выразить его в терминах стандартной нормальной случайной величины Z, используя формулу Z=X−μσZ = frac{X — mu}{sigma}Z=σX−μ. 😎
2. Найти вероятность интервала для стандартной нормальной случайной величины Z, используя таблицы или калькуляторы стандартного нормального распределения. 😍
Пример: Пусть X — это нормально распределенная случайная величина с параметрами μ=50mu = 50μ=50 и σ=10sigma = 10σ=10. Найти вероятность того, что 40<x<6040 <="" x="" 6040<x<60.="" 😊
</x
Решение: 😮
1. Стандартизируем интервал 40<x<6040 <="" x="" 6040<x<60:="" 😯
  То есть, интервал 40<x<6040 <="" x="" 6040<x<60="" соответствует="" интервалу="" −1<z<1-1="" z="" 1−1<z<1="" для="" стандартной="" нормальной="" случайной="" величины="" z.="" 😲
  </x
  </x
2. Найдем вероятность интервала −1<z<1-1 <="" z="" 1−1<z<1="" для="" стандартной="" нормальной="" случайной="" величины="" z,="" используя="" таблицу="" или="" калькулятор="" стандартного="" нормального="" распределения.="" 😍
  По таблице, P(Z<1)≈0.8413P(Z < 1) approx 0.8413P(Z<1)≈0.8413 и P(Z<−1)≈0.1587P(Z < -1) approx 0.1587P(Z<−1)≈0.1587. Тогда, по правилу разности вероятностей, 😎
  По калькулятору, P(−1<z<1)≈0.6827p(-1 <="" z="" 1)="" approx="" 0.6827p(−1<z<1)≈0.6827.="" 😁
  </z
  Таким образом, вероятность того, что 40<x<6040 <="" x="" 6040<x<60="" примерно="" равна="" 0.6826="" или="" 0.6827.="" 😊
  </x
  </z