В этой лекции мы рассмотрим основные понятия и формулы теории вероятностей, которые помогут нам оценивать вероятность различных событий и ситуаций. Мы узнаем, как определить событие, гипотезу, условную вероятность, полную вероятность, априорную и апостериорную вероятность, а также как использовать формулы Бейеса для переоценки вероятности при неизвестных условиях.
- Что такое событие и гипотеза?
- Как определить условную вероятность?
- Как определить полную вероятность?
- Как определить априорную и апостериорную вероятность?
- Как использовать формулы Бейеса?
- Как интерпретировать результаты формул Бейеса?
- Как применять формулы Бейеса на практике?
- Как проверить свои знания по формулам Бейеса?
- Заключение
- 📹 Видео
Видео:Теория вероятностей #11: формула полной вероятности, формула БайесаСкачать

Что такое событие и гипотеза?
Событие – это любое сочетание результатов испытания или наблюдения, которое может произойти или не произойти. Например, событием может быть то, что на экзамене получится более 80 баллов или то, что в магазине нет товара по запросу. События могут быть однозначными (например, выигрыш в лотерее) или неоднозначными (например, температура воздуха).
Гипотеза – это одна из возможных событий или комбинаций событий. Гипотеза представляет собой предположение о том, что может произойти в определенном случае. Например, гипотезой может быть то, что на экзамене получится более 80 баллов или то, что в магазине есть товар по запросу. Гипотезы могут быть однородными (например, все шары равновесны) или неоднородными (например, первый шар не равновесен).
Видео:Формула полной вероятности. Формула Байеса.Скачать

Как определить условную вероятность?
Условная вероятность – это отношение числа между условиями наступления одной из событий и общего числа всех возможных условий. Например, если мы выбираем кубик из трех кубиков по очереди: красный – зеленый – черный; то условная вероятность того, что выбран кубик красного цвета равна 1/3.
Условная вероятность можно выразить как процент от общего числа всех возможных результатов испытания или наблюдения. Например, если мы выбираем кубик из трех кубиков по очереди: красный – зеленый – черный; то общее число всех возможных результатов равно 3^3 = 27 (каждый кубик имеет три возможных цвета). Тогда условная вероятность того, что выбран кубик красного цвета равна 1/27.
Видео:Формула Байеса. Какова вероятность болезни?Скачать

Как определить полную вероятность?
Pолная вероятность – это отношение числа между условиями наступления одной из событий и общего числа всех возможных результатов испытания или наблюдения. Например, если мы выбираем кубик из трех кубиков по очереди: красный – зеленый – черный; то полная вероятность того, что выбран кубик красного цвета равна 1/27.
Pолная вероятность можно выразить как процент от общего числа всех возможных результатов испытания или наблюдения. Например, если мы выбираем кубик из трех кубиков по очереди: красный – зеленый – черный; то общее число всех возможных результатов равно 3^3 = 27 (каждый кубик имеет три возможных цвета). Тогда полная вероятность того, что выбран кубик красного цвета равна 1/27.
Видео:Формула полной вероятности.Скачать

Как определить априорную и апостериорную вероятность?
Априорная вероятность – это вероятность, которая известна до проведения испытания или наблюдения. Априорная вероятность основана на предварительных знаниях или допущениях о событиях или гипотезах. Например, априорной вероятностью может быть то, что в мешке с шариками 50% шариков белые, а 50% шариков черные.
Апостериорная вероятность – это вероятность, которая получается после проведения испытания или наблюдения. Апостериорная вероятность основана на фактических данных или результатх о событиях или гипотезах. Например, апостериорной вероятностью может быть то, что в мешке с шариками 60% шариков белые, а 40% шариков черные, если мы вытащили из мешка 10 шариков и 6 из них оказались белыми.
Видео:Формула полной вероятности. Формула БайесаСкачать

Как использовать формулы Бейеса?
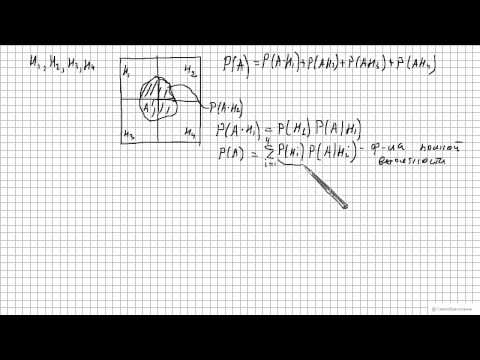
Формулы Бейеса – это набор формул, которые позволяют пересчитать априорную вероятность в апостериорную вероятность при наличии новой информации. Формулы Бейеса основаны на правиле умножения вероятностей и формуле полной вероятности. Формулы Бейеса помогают нам обновлять наши предположения о событиях или гипотезах в свете новых данных или результатов.
Основная формула Бейеса имеет вид:
Где:
- P(H|E) – апостериорная вероятность гипотезы H при условии, что произошло событие E;
- P(E|H) – условная вероятность события E при условии, что верна гипотеза H;
- P(H) – априорная вероятность гипотезы H;
- P(E) – полная вероятность события E.
Пример использования формулы Бейеса:
Предположим, что мы хотим оценить вероятность того, что человек болен определенной болезнью, если у него есть определенный симптом. Допустим, что:
- P(Б) – априорная вероятность болезни, равная 0.01 (1% населения болеет этой болезнью);
- P(С) – полная вероятность симптома, равная 0.05 (5% населения имеет этот симптом);
- P(С|Б) – условная вероятность симптома при условии, что человек болен, равная 0.9 (90% больных имеют этот симптом);
- P(Б|С) – апостериорная вероятность болезни при условии, что человек имеет симптом, которую мы хотим найти.
По формуле Бейеса мы можем найти P(Б|С) следующим образом:
Таким образом, вероятность того, что человек болен, если у него есть симптом, равна 18%. Это гораздо выше, чем априорная вероятность болезни, которая была 1%. Это означает, что наличие симптома значительно повышает вероятность болезни.
Видео:Математика без Ху!ни. Сложение и умножение вероятностей. Формула полной вероятности.Скачать

Как интерпретировать результаты формул Бейеса?
Результаты формул Бейеса показывают, насколько сильно изменяется наша уверенность в гипотезе при наличии новой информации. Чем больше разница между априорной и апостериорной вероятностью, тем больше влияние новой информации на нашу оценку гипотезы. Например, в предыдущем примере разница между априорной и апостериорной вероятностью болезни составила 17%, что говорит о том, что симптом является сильным доказательством болезни.
Однако, результаты формул Бейеса не следует воспринимать как окончательную истину, а скорее как ориентир для дальнейшего исследования. Формулы Бейеса зависят от того, какие априорные вероятности и условные вероятности мы используем в расчетах. Эти вероятности могут быть неточными, неполными или субъективными. Поэтому, важно проверять и обновлять наши вероятности по мере поступления новых данных или результатов.
Видео:Формула полной вероятности. Формула БайесаСкачать
Как применять формулы Бейеса на практике?
Формулы Бейеса имеют широкое применение в различных областях знания и деятельности. Например, формулы Бейеса используются для:
- Диагностики болезней и лечения пациентов;
- Прогнозирования погоды и климата;
- Анализа рынков и инвестиций;
- Распознавания речи и изображений;
- Фильтрации спама и мошенничества;
- Обучения искусственного интеллекта и машинного обучения;
- И многого другого.
Формулы Бейеса помогают нам делать более обоснованные и рациональные решения на основе доступной информации. Однако, формулы Бейеса не являются панацеей от всех проблем и несут в себе определенные ограничения и трудности. Поэтому, важно критически оценивать наши вероятности и результаты, а также учитывать другие факторы, такие как здрав ый смысл, интуицию и этику.
Видео:✓ Формула Байеса в реальной жизни | Математика вокруг нас | Борис ТрушинСкачать

Как проверить свои знания по формулам Бейеса?
Для того, чтобы закрепить свои знания по формулам Бейеса, вы можете попробовать решить несколько простых задач, которые иллюстрируют применение формул Бейеса на практике. Вот несколько примеров таких задач:
- В классе 30 учеников, из них 15 девочек и 15 мальчиков. Из 15 девочек 10 носят очки, а из 15 мальчиков 5 носят очки. Какова вероятность того, что случайно выбранный ученик из этого класса будет девочкой, если известно, что он носит очки?
- В мешке 10 монет, из них 4 правильные и 6 фальшивых. Правильная монета выпадает орлом или решкой с равной вероятностью 0.5, а фальшивая монета выпадает орлом с вероятностью 0.9 и решкой с вероятностью 0.1. Какова вероятность того, что монета, выбранная из мешка, будет правильной, если при подбрасывании она выпала орлом?
- В тесте по английскому языку 20 вопросов, из них 10 легких и 10 сложных. Студент знает ответ на легкий вопрос с вероятностью 0.8, а на сложный вопрос с вероятностью 0.4. Какова вероятность того, что студент знает ответ на случайно выбранный вопрос, если известно, что он ответил на него правильно?
Вы можете попытаться решить эти задачи самостоятельно, используя формулы Бейеса, или проверить свои ответы с помощью интернет-ресурсов, таких как этот.
Видео:Формула полной вероятности и формулы БайесаСкачать

Заключение
В этой лекции мы изучили основные понятия и формулы теории вероятностей, которые помогают нам оценивать вероятность различных событий и ситуаций. Мы узнали, как определить событие, гипотезу, условную вероятность, полную вероятность, априорную и апостериорную вероятность, а также как использовать формулы Бейеса для переоценки вероятности при неизвестных условиях. Мы также рассмотрели, как интерпретировать результаты формул Бейеса и как применять их на практике в различных областях знания и деятельности. Наконец, мы предложили вам несколько задач для проверки своих знаний по формулам Бейеса.
Надеемся, что эта лекция была полезной и интересной для вас, и вы смогли узнать что-то новое и важное о теории вероятностей и формулах Бейеса. Спасибо за внимание и удачи в дальнейшем обучении! 😊
📹 Видео
08 Формула полной вероятности ЗадачиСкачать

Теорема Байеса [3Blue1Brown]Скачать
![Теорема Байеса [3Blue1Brown]](https://i.ytimg.com/vi/_bcAK_1a72k/0.jpg)
Найти вероятность по формуле Байеса (Бейеса)Скачать

ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛЫ БАЙЕСАСкачать

Формулы полной вероятности и формулы Байеса. Лекция 4.Скачать

Условная вероятность #1: формула БайесаСкачать

Решение задач на тему "Формула полной вероятности. Формула Байеса"Скачать

Решение задач по теории вероятностей | Часть 2 | Формула полной вероятности и формула БайесаСкачать

Формулы полной вероятности и БайесаСкачать

Формула полной вероятности. Формула Байеса.Скачать

Формула полной вероятности. Формула Байеса (1)Скачать