Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признакаоднородных единиц совокупности.
Величина средней дает обобщающую количественную характеристику всей совокупности и характеризует ее в отношении данного признака.
Так, например, средняя заработная плата дает обобщающую количественную характеристику состояния оплаты труда рассматриваемой совокупности работников.
Кроме того, используя средние величины, имеется возможность сопоставлять различные информационные совокупности.
Так, например, можно сравнивать различные организации по уровню производительности труда, а также по уровню фондоотдачи, материалоотдачи и по другим показателям.
Сущность средней заключается в том, что в ней взаимопогашаются случайные отклонения значений признака и учитываются изменения вызванные основным фактором.
Статистическая обработка методом средних величин заключается в замене индивидуальных значений варьирующего признака некоторой уравновешенной средней величиной .
Например, индивидуальная выработка у 5 операционистов коммерческого банка за день составила 136, 140, 154 и 162 операции. Чтобы получить среднее число операций за день, выполненных одним операционистом, необходимо сложить эти индивидуальные показатели и полученную сумму разделить на количество операционистов:
операций.
Как видно из приведенного примера, среднее число операций не совпадает ни с одним из индивидуальных, так как ни один операционист не сделал 150 операций.
Но если мы представим себе, что каждый операционист сделал по 150 операций, то их общая сумма не изменится, а будет также равна 750.
Таким образом, мы пришли к основному свойству средних величин: сумма индивидуальных значений признака равна сумме средних величин.
Это свойство еще раз подчеркивает, что средняя величина является обобщающей характеристикой всей статистической совокупности.
Средние величины широко применяются в различных отраслях знаний. Особо важную роль они играют в экономике и статистике: при анализе, планировании, прогнозировании, при расчете нормативов и при оценке достигнутого уровня. Средняя всегда именованная величина и имеет ту же размерность, что и отдельная единица совокупности.
- Важнейшими условиями (принципами) для правильного вычисления и использования средних величин является следующие:
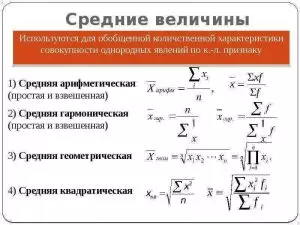
- Виды средних величин
- Расчет некоторых средних величин:
- Степенные средние величины
- Формула степенной простой в общем виде
- Формула степенной средней взвещенной в общем виде
- Средняя величина в статистике — это… Средние величины
- Средняя величина — это что такое?
- Зачем она используется?
- Сферы применения
- Средняя величина в статистике
- Как правильно рассчитать
- Условия правильного вычисления
- Классы СВ
- Виды степенных СВ
- Виды структурных величин
- Средние величины в статистике: сущность, свойства, виды. Примеры решения задач
- Виды средних величин, используемых в статистике
- Примеры решения задач по теме «Средние величины в статистике»
- 💥 Видео
Важнейшими условиями (принципами) для правильного вычисления и использования средних величин является следующие:
- В каждом конкретном случае необходимо исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков и имеющиеся для расчета данные.
- Индивидуальные значения, из которых вычисляются средние, должны относиться к однородной совокупности, а число их должно быть значительным.
Виды средних величин
Средние величины делятся на два больших класса: степенные средние и структурные средние
Степенные средние:
- Арифметическая
- Гармоническая
- Геометрическая
- Квадратическая
Структурные средние:
Выбор формы средней величины зависит от исходной базы расчета средней и от имеющейся экономической информации для ее расчета.
Исходной базой расчета и ориентиром правильности выбора формы средней величины являются экономические соотношения, выражающие смысл средних величин и взаимосвязь между показателями.
Расчет некоторых средних величин:
- Средняя заработная плата 1 работника = Фонд заработной платы / Число работников
- Средняя цена 1 продукции = Стоимость производства / Количество единиц продукции
- Средняя себестоимость 1 изделия = Стоимость производства / Количество единиц продукции
- Средняя урожайность = Валовый сбор / посевная площадь
- Средняя производительность труда = объем продукции, работ, услуг / Отработанное время
- Средняя трудоемкость = отработанное время / объем продукции, работ, услуг
- Средняя фондоемкость = Средняя стоимость основных фондов / объем продукции, работ и услуг
- Средняя фондоотдача = объем продукции, работ и услуг / средняя стоимость основных фондов
- Средняя фондовооруженность = средняя величина основных производственных фондов / среднесписочная численность производственного персонала
- Средний процент брака = ( стоимость бракованной продукции / Стоимость всей произведенной продукции ) * 100%
Степенные средние величины
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.
Если вариант встречается один раз, расчеты проводим по средней простой (например зарплата в 3 тыс.руб.
встречается только у одного рабочего), а если вариант повторяется неодинаковое число раз, то есть имеет разные частоты (например зарплата в 4 тыс.рублей встречается у пяти работников), то расчет проводим по средней взвешенной.
Формула степенной простой в общем виде
где:
- — индивидуальное значение признака -й единицы совокупности
- — показатель степени средней величины
- — число единиц совокупности
Формула степенной средней взвещенной в общем виде
где:
- — частота повторения -й варианты.
В зависимости от того, какое значение принимает показатель степени средней величины , получаем различные виды средних:
При расчете различных степенных средних по одним и тем же данным значения средних будут неодинаковыми. Чем выше показатель степени (), тем больше величина средней, т.е. действует правило мажорантности средних:
Видео:Средние величины - арифметическая и гармоническая взвешенныеСкачать

Средняя величина в статистике — это… Средние величины
Каждый человек в современном мире, планируя взять кредит или делая запасы овощей на зиму, периодически сталкивает с таким понятием, как «средняя величина». Давайте узнаем: что это такое, какие ее виды и классы существуют и зачем она применяется в статистике и других дисциплинах.
Средняя величина — это что такое?
Подобное название (СВ) носит обобщенная характеристика совокупности однородных явлений, определяемая по какому-либо одному количественному варьируемому признаку.
Однако люди далекие, от столь заумных определений, понимают это понятие, как среднее количество чего-то.
Например, прежде чем взять кредит, сотрудник банка обязательно попросит потенциального клиента предоставить данные о среднем доходе за год, то есть общую сумму зарабатываемых человеком средств.
Она вычисляется путем суммирования заработанного за весь год и разделения на количество месяцев. Таким образом, банк сможет определить, сумеет ли его клиент отдать долг в срок.
Зачем она используется?
Как правило, средние величины широко применяются для того, чтобы дать итоговую характеристику определенных общественных явлений, носящих массовый характер. Также они могут быть использованы для менее масштабных расчетов, как в случае с кредитом, в приведенном выше примере.
https://www.youtube.com/watch?v=bC9tHZlrji0
Однако чаще всего средние величины все же применяются для глобальных целей. В качестве примера одного из них можно привести вычисление количества потребляемой гражданами электроэнергии на протяжении одного календарного месяца. На основе полученных данных в дальнейшем устанавливаются максимальные нормы для категорий населения, пользующихся льготами от государства.
Также с помощью средних величин разрабатывается гарантийный срок службы тех или иных бытовых приборов, автомобилей, зданий и т. п. На основе собранных таким способом данных когда-то были разработаны современные нормы труда и отдыха.
Фактически любое явление современной жизни, носящее массовый характер, тем или иным образом обязательно связано с рассматриваемым понятием.
Сферы применения
Данное явление широко применяется практически во всех точных науках, особенно носящих экспериментальный характер.
Поиск среднего значения величины имеет огромное значение в медицине, инженерных дисциплинах, кулинарии, экономике, политике и т. п.
Основываясь на данных, полученных от подобных обобщений, разрабатывают лечебные препараты, учебные программы, устанавливают минимальные прожиточные минимумы и зарплаты, строят учебные графики, производят мебель, одежду и обувь, предметы гигиены и многое другое.
В математике данный термин именуется «средним значением» и применяется для осуществления решений различных примеров и задач. Наиболее простыми из них являются сложение и вычитание с обычными дробями. Ведь, как известно, для решения подобных примеров необходимо привести обе дроби к общему знаменателю.
Также в царице точных наук часто применяется близкий по смыслу термин «значение среднее случайной величины». Большинству он более знаком как «математическое ожидание», чаще рассматриваемое в теории вероятности. Стоит отметить, что подобное явление также применяется и при произведении статистических вычислений.
Средняя величина в статистике
Однако чаще всего изучаемое понятие используется в статистике. Как известно, эта наука сама по себе специализируется на вычислении и анализе количественной характеристики массовых общественных явлений. Поэтому средняя величина в статистике используется в качестве специализированного метода достижения ее основных задач — сбора и анализа информации.
Суть данного статистического метода заключается в замене индивидуальных уникальных значений рассматриваемого признака определенной уравновешенной средней величиной.
В качестве примера можно привести знаменитую шутку о еде. Итак, на неком заводе по вторникам на обед его начальство обычно ест мясную запеканку, а простые рабочие – тушеную капусту. На основе этих данных можно сделать вывод, что в среднем коллектив завода по вторникам обедает голубцами.
Хотя данный пример слегка утрирован, однако он иллюстрирует главный недостаток метода поиска средней величины – нивелирование индивидуальных особенностей предметов или личностей.
В статистике, данные средних величин применяются не только для анализа собранной информации, но и для планирования и прогнозирования дальнейших действий.
Также с его помощью производится оценка достигнутых результатов (например, выполнение плана по выращиванию и сбору урожая пшеницы за весенне-летний сезон).
Как правильно рассчитать
Хотя в зависимости от вида СВ существуют разные формулы ее вычисления, в общей теории статистики, как правило, применяется всего один способ расчета средней величины признака.
Для этого нужно сначала сложить вместе значения всех явлений, а затем разделить получившуюся сумму на их количество.
При произведении подобных вычислений стоит помнить, что средняя величина всегда имеет ту же размерность (или единицы измерения), что и отдельная единица совокупности.
Условия правильного вычисления
Рассмотренная выше формула весьма проста и универсальна, так что ошибиться в ней практически невозможно. Однако всегда стоит учитывать два аспекта, иначе полученные данные не будут отражать реальную ситуацию.
- Искомые индивидуальные значения (на основе которых вычисляются средние) всегда должны относиться к однородной совокупности, а количество их должно быть значительным. В вышеупомянутой шутке мясная запеканка и капуста – относятся к одной категории – «еда». Однако если бы нужно было узнать, сколько килограмм капусты хранится в столовой завода, учитывать данные о мясе не было бы смысла, так как в данном случае они не относились бы к рассматриваемой однородной совокупности.
- В любом индивидуальном случае важно брать во внимание качественное содержания признака, среднюю величину которого необходимо рассчитать. При этом важно обращать внимание на взаимосвязь между изучаемыми признаками и имеющиеся для вычислений данные.
Классы СВ
Найдя ответы на основные вопросы: «Средняя величина — это что такое?», «Где применяется она?» и «Как можно вычислить ее?», стоит узнать, какие классы и виды СВ существуют.
https://www.youtube.com/watch?v=qptm12VSb88
Прежде всего это явление делится на 2 класса. Это структурные и степенные средние величины.
Виды степенных СВ
Каждый из вышеперечисленных классов, в свою очередь, делится на виды. У степенного класса их четыре.
- Средняя арифметическая величина – это наиболее распространенный вид СВ. Она являет собою среднее слагаемое, при определении коего общий объем рассматриваемого признака в совокупности данных поровну распределяется между всеми единицами данной совокупности. Этот вид делится на подвиды: простая и взвешенная арифметическая СВ.
- Средняя гармоническая величина – это показатель, обратный средней арифметической простой, вычисляемый из обратных значений рассматриваемого признака. Она применяется в тех случаях, когда известны индивидуальные значения признака и произведение, а данные частоты — нет.
- Средняя геометрическая величина чаще всего применима при анализе темпов роста экономических явлений. Она дает возможность сохранять в неизменном виде произведение индивидуальных значений данной величины, а не сумму. Также бывает простой и взвешенной.
- Средняя квадратическая величина используется при расчете отдельных показателе показателей, таких как коэффициент вариации, характеризующего ритмичность выпуска продукции и т. п. Также с ее помощью вычисляются средние диаметры труб, колес, средние стороны квадрата и подобных фигур. Как и все остальные виды средних СВ, среднеквадратическая бывает простой и взвешенной.
Виды структурных величин
Помимо средних СВ, в статистике довольно часто используются структурные виды. Они лучше подходят для расчета относительных характеристик величин варьирующего признака и внутреннего строения рядов распределения.
Таких видов существует два.
- Мода. Данный вид чаще всего используется для определения наиболее популярных у покупателей размеров одежды и обуви. Как правило, мода вычисляется по такой формуле. В ней М0 – является значением моды, х0 – нижней границей интервала модального, h – величиной рассматриваемого интервала, fm – его частотой, fm-1 – частотой предшествующего модальному интервалу и fm+1 – частотой следующего.
- Медианой именуется значение признака, лежащее в основе ранжированного ряда и делящее его на две части, равные между собою по численному показателю. В формулах, данный вид обозначается, как Ме.В зависимости от того в каком ряду определяется данный вид структурной СВ (дискретный или интервальный вариационный), применяются различные формулы его вычисления.
Видео:Средние величины. Средняя арифметическая.Скачать
Средние величины в статистике: сущность, свойства, виды. Примеры решения задач
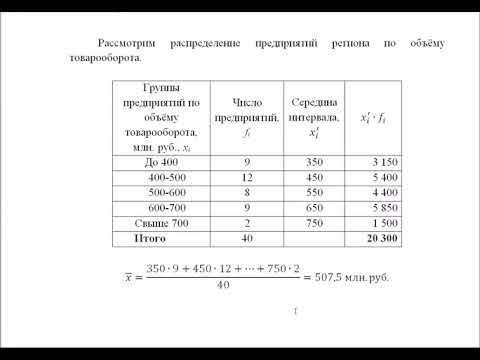
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности, ведь значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть и случайные.
Приведем примеры экономических показателей, основанных на вычислении средней величины и раскрывающих ее сущность:
- расчет средней заработной платы работников предприятия осуществляется делением общего фонда заработной платы на число работников;
- средний размер вклада в банке находят делением суммы вкладов в денежном выражении на количество вкладов;
- для определения средней дневной выработки одного работника необходимо объем работ (количество деталей), выполненных работником за определенный период разделить на число дней в этом периоде.
Виды средних величин, используемых в статистике
Рассмотрим основные виды средних величин, используемых при решении социально-эконмических и аналитических задач.
Средняя арифметическая простая вычисляется по формуле:
Средняя арифметическая простая используется в тех случаях, когда расчет осуществляется по не сгруппированным данным. Пример применения формулы средней арифметической простой представлен в задаче 1.
Средняя арифметическая взвешенная определяется по формуле:
При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам. Пример применения формулы средней арифметической взвешенной представлен в задаче 2.
Средняя гармоническая простая определяется по формуле:
Средние гармонические используются тогда, когда по экономическому содержанию имеется информация для числителя, а для знаменателя ее необходимо предварительно определить.
Средняя гармоническая взвешенная определяется по формуле:
Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса W за ряд временных интервалов. Пример применения формулы средней гармонической взвешенной представлен в задаче 3.
Средняя геометрическая простая (невзвешенная) опеределяется по формуле:
Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста.
Средняя квадратическая простая (невзвешенная) опеределяется по формуле:
Средняя квадратическая лежит в основе вычислений ряда сводных расчетных показателей.
https://www.youtube.com/watch?v=xXBPqdcnXz4
Наиболее часто используемыми в экономической практике структурными средними являются мода и медиана.
Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.
Медианой (Ме) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Пример определения медианы и моды для дискретного ряда чисел представлен в задаче 1.
Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.
Для интервального ряда расчет моды осуществляется по формуле:
где Хо — нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); i — величина модального интервала; f Мо — частота модального интервала; f Мо-1 — частота интервала, предшествующего модальному; f Мо+1 — частота интервала, следующего за модальным.
Для интервального ряда расчет медианы осуществляется по формуле:
Хо — нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); i — величина медианного интервала; Sme-1 — накопленная частота интервала, предшествующего медианному; f Me — частота медианного интервала.
Примеры решения задач по теме «Средние величины в статистике»
Задача 1. Дан ряд чисел: 15; 15; 12; 14; 13. Найдите размах, среднее арифметическое, медиану и моду этого ряда.
Решение
1) Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел. В данном случае размах равен R = 15-12 = 3
2) Среднее арифметическое данного ряда находим по формуле средней арифметической простой. Хср = (15+15+12+14+13)/5=13,8
3) Для определения медианы необходимо предложенный ряд упорядочить – расположить числа, например, в порядке возрастания: 12; 13; 14; 15; 15.
Медиана нечетного количества чисел в дискретном ряде – это число, записанное посередине. Медиана четного количества чисел – это среднее арифметическое двух чисел, находящихся посередине.
Поскольку в нашем случае количество чисел ряда нечетноне, то Ме = 14.
4) Мода дискретного ряда чисел – это число, которое встречается в данном ряде чаще других. Так как число 15 встречается в нашем ряде чаще других, то Мо = 15.
Задача 2. Имеется информация о численности студентов ВУЗов города и удельном весе (%) обучающихся студентов на коммерческой основе:
Определить: 1) средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе; 2) число этих студентов.
Решение
Для решения расширим предложенную таблицу:
Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе определим по формуле средней арифметической взвешенной: Хср = (15×15+3×10+7×20) / (15+3+7) = 15,8%.
Ответ. Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе равен 15,8%, число этих студентов – 3 950 человек.
Задача 3. Сумма невыплаченной своевременно задолженности по кредитам на 1 июля составила 92,4 млн. денежных единиц. По отдельным отраслям экономики она распределялась следующим образом:
Определить средний процент невыплаченной своевременно задолженности. Обоснуйте выбор формы средней.
Решение
Поскольку на различных предприятиях сумма задолженности по кредитам разная при разных удельных весах, то применим формулу средней гармонической взвешенной.
Хср = ΣW / Σ(W/х) = (32+14+46,4)/(32/20+14/28+46,4/16) = 92,4/5 = 18,48 %.
Ответ. Средний процент невыплаченной своевременно задолженности равен 18,48%.
Список использованных источников
- Белобородова С.С. и др. Теория статистики: Типовые задачи с контрольными заданиями. Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2001;
- Минашкин В.Г. и др. Курс лекций по теории статистики. / Московский международный институт эконометрики, информатики, финансов и права. — М., 2003;
- Сизова Т.М. Статистика: Учебное пособие. – СПб.: СПб ГУИТМО, 2005;
- Фёдорова Л.Н., Фёдорова А.Е. Методические указания по написанию контрольной работы по курсу «Статистика» для студентов экономических специальностей: УрГЭУ, 2007;
💥 Видео
Статистика. Средние величиныСкачать

Математическое Ожидание, Дисперсия, Стандартное Отклонение за 5 минутСкачать

Средние величины в статистикеСкачать

Структурные средниеСкачать

Элементы статистики. Дисперсия. Стандартное отклонениеСкачать

Средние величины. Средняя гармоническая.Скачать

Средние величины. Средняя геометрическая.Скачать

Статистика с нуля за 5 минут ПРОСТЫМИ СЛОВАМИСкачать

Мода, размах, среднее арифметическое, медианаСкачать

Статистика. Средние величины. Разбор задачи 20Скачать

Статистика. Средние величины. Разбор задачи 41Скачать

Статистика. Средние величины. Разбор задачи 37Скачать

Абсолютные и относительные величины, часть 2Скачать

Распределение в Статистике за 5 МинутСкачать

Средние величины. Средняя квадратическая.Скачать

Статистика без галстука - СредниеСкачать

Нормальное Распределение за 6 МинутСкачать

Статистика. Формулы нахождения средних величинСкачать